ł∂ņÔ»~∑÷őŲļÕł∂ņÔ»~Ļ‚ĆW(xu®¶)
ģĒ(d®°ng)«įőĽ÷√£ļ ◊Ūď >> Éx∆ųÉxĪŪľľ–g(sh®ī)őń’¬
ł∂ņÔ»~∑÷őŲļÕł∂ņÔ»~Ļ‚ĆW(xu®¶)
į—“ĽāÄŹÕ(f®ī)ŽsĶń’ŮĄ”ĽÚ∆šňŁ÷‹∆ŕŖ^≥Ő”√ł∂ņÔ»~ľČĒĶ(sh®ī)∑÷Ĺ‚ěťłų∑NÓl¬ ≥…∑÷÷C≤®ĶńĮBľ”£ĽĆ¶∑«÷‹∆ŕĶń≤®Ą”ļĮĒĶ(sh®ī)£¨ĄtŅ…”√ł∂ņÔ»~∑e∑÷∑Ĺ∑®ĆĘļĮĒĶ(sh®ī)∑÷Ĺ‚ěť–ÚŃ–ŖBņm(x®ī)ĽÚ≤ĽŖBņm(x®ī)ĶńļÜ÷C≤®Ķń°įŖBņm(x®ī)ļÕ°Ī£¨Ŗ@∑N∑Ĺ∑®∑Qěťł∂ņÔ»~∑÷őŲĽÚÓl◊V∑÷őŲ°£–ŇŐĖ÷–łų∑NÓl¬ ≥…∑÷Ķńļ¨ŃŅ£¨ĺÕ∑Qěť–ŇŐĖĶńÓl◊V£¨ļÜ∑Q◊V°£
»ÁÕ¨ŽäīŇ≤®Ņ…“‘ŖM(j®¨n)––ērťg’{(di®§o)÷∆ļÕŅ’ťg’{(di®§o)÷∆“Ľė”£¨Ļ‚≤®“≤”–ērťg’{(di®§o)÷∆ļÕŅ’ťg’{(di®§o)÷∆°£ģĒ(d®°ng)≤…”√Ņ’ťg’{(di®§o)÷∆ēr£¨∑÷őŲ≤®Ķńāų≤•£¨≥£‘ŕŅ’”ÚĽÚŅ’Ól”ÚŖM(j®¨n)––£ĽģĒ(d®°ng)≤…”√ērťg’{(di®§o)÷∆ēr£¨∑÷őŲ≤®Ķńāų≤•£¨≥£‘ŕēr”ÚĽÚērÓl”ÚŖM(j®¨n)––°£‘ŕŅ’”Ú÷–£¨Ļ‚≤® «Õ®Ŗ^›Ē»Ž∆Ĺ√śŖM(j®¨n)––āų≤•Ķń£¨∆šŹÕ(f®ī)’Ů∑ýĪŪ ĺěť›Ē»Ž∆Ĺ√śĶńŅ’ťg◊Ýėň(bi®°o)x£¨yĶńļĮĒĶ(sh®ī)°£»ÁĻŻį—ł∂ņÔ»~∑÷őŲĶńĽýĪĺ∂®ņŪĎ™(y®©ng)”√ĶĹĻ‚ń‹∑÷≤ľĶń∑÷őŲ÷–£¨ĺÕŅ…“‘ĆĘ»ő“‚∂ĢĺSŹÕ(f®ī)’Ů∑ýļĮĒĶ(sh®ī)£¨∑÷Ĺ‚ěťłų∑N–ÚŃ–ŖBņm(x®ī)ĽÚ≤ĽŖBņm(x®ī)Ķń”ŗŌ“(ĽÚ’żŌ“)≤®ĶńĮBľ”°£”“ąDĹo≥ŲŃň∑Ĺ≤®Ķńł∂ņÔ»~∑÷őŲąDņż°£
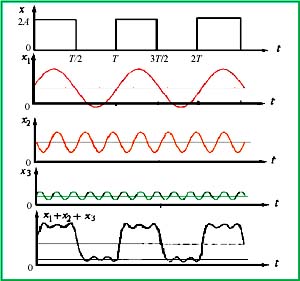
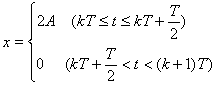
ƶ…Ō ĹŖM(j®¨n)––ł∂ņÔ»~∑÷őŲ£¨Ņ…Ķ√£ļ
∆š÷–£ļ¶ō=2¶–/T
”…īňŅ…“䣨ł∂ņÔ»~∑÷őŲŅ…“‘į—“Ľį„Ļ‚≤®∑÷Ĺ‚ěť‘S∂ŗ∆Ĺ√ś≤®ĶńĮBľ”°£Ć¶∆Ĺ√ś≤®āų≤•ļÕ—‹…šĶń∑÷őŲŌŗƶ›^ěťļÜÜő£¨“Ú∂Ý£¨ł∂ņÔ»~∑÷őŲ≥…ěťĻ‚ĆW(xu®¶)—–ĺŅ ģ∑÷”–”√ĶńĻ§ĺŖ°£
ĆĘĻ‚ĆW(xu®¶)ąDŌŮ»ÁÕ¨Žä–ŇŐĖ“Ľė”ŖM(j®¨n)––ł∂ņÔ»~∑÷őŲ£¨į—∑«≥£≥… žĶńÕ®–ŇņŪ’ďļÕ∑Ĺ∑®Ŗ\(y®īn)”√ĶĹĻ‚ĆW(xu®¶)÷–£¨–ő≥…Ńň“ĽťT–¬ĆW(xu®¶)Ņ∆°™ł∂ņÔ»~Ļ‚ĆW(xu®¶)°£
įl(f®°)≤ľ»ň£ļ2010/7/5 10:29:001081
įl(f®°)≤ľērťg£ļ2010/7/5 10:29:00
īň–¬¬Ą“—ĪĽěg”[:1081īő
łŁ∂ŗŌŗÍP(gu®°n)–ŇŌĘ
- »ÁļőŹńPARī_∂®DLI£®√Ņ»’Ļ‚∑e∑÷£©
- úyŃŅúō “÷–Ķń»’Ļ‚∑e∑÷(DLI)…ŐėI(y®®)úō “Ď™(y®©ng)”√
- łŁďQU26-001»‹Ĺ‚—ű”õšõÉxāųł–∆ų√ĪU26-RDOB-1Ķń≤Ŕ◊ų≤ĹůE
- ‘uĻņ∂Ģ—űĽĮŐľĒĶ(sh®ī)ďĢ(j®ī)”õšõ∆ųĶń5āÄ÷ō“™ŅľĎ]“Úňō
- ļ£—ůö‚úō◊ÉĽĮ «∑ŮēĢ÷ķŹä(qi®Ęng)ÔZÔL(f®•ng)
- –¬–Õ”õšõÉxMX2200ŌĶŃ–Ķń“Ľ–©ÜĖÓ}ļÕĹ‚īū
- ň{(l®Ęn)—ņňģőĽ”čMX2001≤ĽÕ¨ňģőĽÖĘŅľŁc(di®£n)ĶńŖx»°ļÕÖĘŅľňģőĽ÷Ķ‘O(sh®®)÷√’f√ų‘ĒĹ‚
- OnsetĶńŔ|(zh®¨)ŃŅĻ‹ņŪůwŌĶ
- ’Łĺ»…ļļųĹł“ĽāÄ”¬ł“Ķń–¬ ņĹÁ…ļļųĹł
- ÕŃ»ņňģ∑÷āųł–∆ųS-SMD-M005ļÕS-SMC-M005Ļ§◊ų‘≠ņŪÉě(y®≠u)Łc(di®£n)ļÕÖ^(q®Ī)Ąe
∑÷ÓźŁc(di®£n)ďŰŇŇ––
- 1500√◊∑ņňģúō∂»”õšõÉxMX2204 HOBO TidbiT MX Tempe 5000
- HOBOüoĺÄň{(l®Ęn)—ņňģŌ¬úō∂»”õšõÉxMX2203 TidbiT MX
- MX2201–¬ŅÓéßň{(l®Ęn)—ņňģŌ¬úō∂»”õšõÉxPendant MX Temp
- ∑ņĽūąůĺĮ÷«ń‹üŠŌŮFotric816/Fotric826
- Ļ§≥ŐéüÕ®”√üŠŌŮÉxFotric 222s/Fotric 222s-1/Fotric 222s-2
- HOBO MX100ň{(l®Ęn)—ņúō∂»”õšõÉx∑ņňģĶ»ľČIP67
- Ņ…≥Ő Ĺ‘Ž“Ű”čTES-1352Séß”õšõŅ…≤ŚSDŅ®
- ĒĶ(sh®ī)ďĢ(j®ī)”õšõ–Õ’’∂»Ļ‚ŃŅ◊””čTES-1339P
- Ī„Ēy“Ľůw ĹúōĚŮ∂»īůö‚ČļѶ”čTES-1160/TES-1161
- łŖĺę∂»ňģőĽ”čMX2001-04-séßüoĺÄĒĶ(sh®ī)ďĢ(j®ī)āų›Ē


